Если ранее коэффициенты были найдены при заданных функциях (pfe, то в данном случае эти коэффициенты зависят от ак (k = 1, 2, п) как от параметров, т. е. sn(x) = s„(x, ах,ап). Параметры ак могут быть найдены из условия минимума
получим
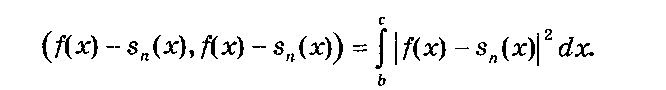
Так как f(x) = f(x) - sn(x) + sn(x), a sn(x) и f(x) - sn(x) ортогональны, т. e. (f(x) - sn(x), sn(x)) = 0, то (f(x), f(x)) = (f(x) -s„(*)> fix) - sn(x)) + isn(x), sn(x)).
Условие минимума (f(x) - sn(x), f(x) - sn(x)) сводится к условию максимума (s„(*), snix)) = ||sn(*)||2 квадрата нормы
функции. Таким образом, параметры {ак}" определяются
из системы уравнений:
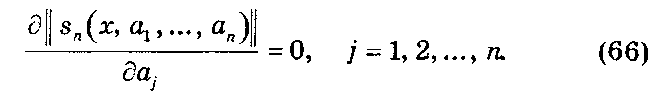
Увеличивая число параметров, можно прийти к последовательности {а}, которая по теореме Больцмана—Коши обязательно будет содержать конечную и бесконечную точку сгущения, а значит, приведет к системе функций {ц>к} со свойствами, необходимыми для разложения в ряд непрерывных функций.
Теперь можно показать на простых примерах возможность реализации принципа двойственности, в которой качественность может заменяться количественностыо1. Действительно, если некоторую функцию f(x) представим сходящимся степенным рядом вида:
fix) = т0 + тхх + т2хг + ... + тпхп, (67)
где т0, т1, т2, тп — постоянные коэффициенты, то в принципе, реализация функции может быть осуществлена соответствующим подбором масштабных коэффициентов.
Поскольку лекарственные препараты не являются степенными функциями, а являются также неизвестными функциями, то мы можем записать формулу (67) в виде:
faix) = т'0 + т[Ъ(х) + m'2f2(x) + ... + m'Jnix). (68) Разложим функции (67) в сходящиеся степенные ряды
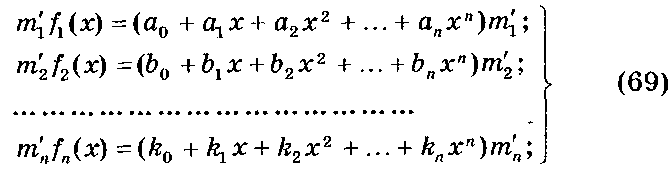
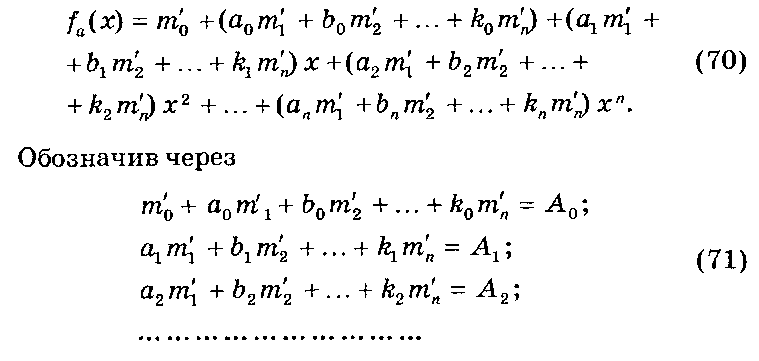
Запишем выражение (68) с учетом (69):
fa(x)=A0+A1x+A2x2 + ... + Anxn. (72)
Сравнивая функции f(x) и fa(x), легко заметить, что они отличаются одна от другой постоянными коэффициентами.
Исходя из приведенного математического обоснования, можно заключить, что хотя элементы, воспроизводящие х, х2, х3,х", &такжеА0,А1,А2, ...,Ап, обладают нелинейностью, возможно с необходимой для практики точностью подобрать такие коэффициентыА0,А1,А2, ...,Ап, при которых воспроизводимая функция fa(x) настраивалась бы на заданную f(x), т. е.
Peклaмa:
