Используя теорему единственности теории функций комплексного переменного [4], можно получить более общий результат. Эта теорема утверждает, что если аналитическая функция обращается в нуль на последовательности точек, сходящихся к внутренней точке, т. е. принадлежащей области аналитичности, то такая функция обращается в нуль во всей области аналитичности. В нашем случае выберем множество {(х - а,,)1}, где значения ап не принадлежат отрезку [Ь, с], различны и сходятся к любой точке вне отрезка [Ь, с], т. е. последовательность может содержать несколько последовательностей, сходящихся к различным точкам.
Функция f(x), ортогональная множеству {(х - а„)-1}, обратит аналитическую функцию F(z) в точках а„ в нуль по теореме единственности. Тогда функция F(z) равна нулю вне отрезка [Ь, с]. Повторяя предыдущие рассуждения, приходим к выводу, что линеал множества {(х - а„)-1} плотен в классе непрерывных функций.
Итак, любая непрерывная функция f(x) может быть разложена в ряд по функциям (х - ап)~\ где {а„} сходится к точке вне [Ь, с], в частности, к бесконечно удаленной точке
ао q
f(x) = ^ —-—, где сходимость описывается выражением:
к=1 х ~ ак
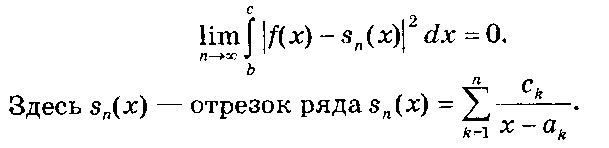
Полученное разложение имеет следующее необычное свойство: его коэффициенты однозначно не определяются. Действительно, если в множестве {(х - а„)-1} отбросить любое конечное число функций, то в оставшемся множестве совокупность ап удовлетворяет теореме единственности и, следовательно, линеал по полученному множеству снова плотен в классе непрерывных функций.
Пусть отброшено п первых функций (х - а„)-1. Рассмот-
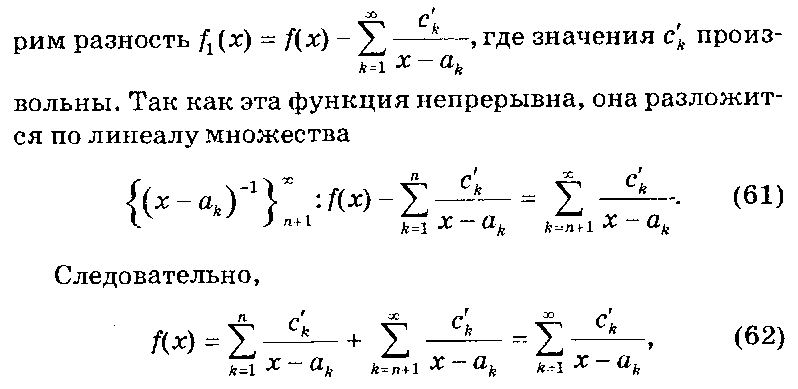
где c'k (k - 1, 2, п) произвольны. Таким образом, разложение оказывается неоднозначным.
До настоящего времени вопрос о сходимости изучался с точки зрения среднеквадратичного отклонения [6]. Исследуем возможность сходимости ряда при некотором зафиксированном значении х из интервала [Ь, с].

дится к f(x) в смысле L2, то он сходится к f(x) почти всюду в отрезке [Ь, с]. Это означает, что для любого сколь угодно малого е > 0 мера множества значений х из отрезка [Ь, с], для которых \f(x) -sa(x)\ > е стремится к нулю при п -> со.
Обозначим через Еп множество значений х, для которых |/(х) - sn(x)\ > g, а через тЕп — меру Еп. Тогда:
следуемого при рассмотрении вопроса о плотности системы {ехр ах) в пространстве непрерывных функций. Поэтому здесь уже нельзя выбирать последовательность {ак}, стремящуюся к бесконечно удаленной точке. Выше было установлено, что любую непрерывную функцию f(x), где х е [Ь, с], можно разложить в ряд в смысле Ьг по системе {(х - а)"1}. Введя обозначение (pk = (х - a J-1, получим разложение вида
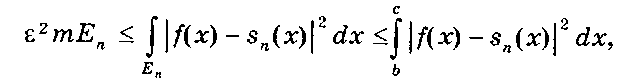
где интеграл по Еп берется по Лебегу [6]. Второй интеграл этого выражения при п -н> со стремится к нулю. Отсюда тпЕп -> 0 и сходимость почти всюду доказана. К сожалению, равномерную сходимость из сходимости в смысле L2 и аналитичности функций f(x) и sn{x) вывести нельзя.
Peклaмa:
