Действительно, возьмем sn(x) = хп. На отрезке [0, 1], х" -> 0 при п ф 1 ихп-> 1 при п = 1, когда п -> оои в то же время стремится к нулю в смысле L2, так как
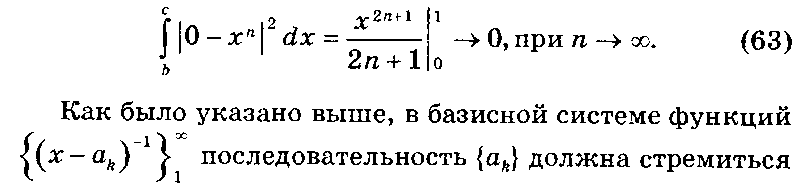
к точке а, в которой интеграл типа Коши аналитичен. Если значение а конечно, то точки ак, начиная с некоторого номера N, будут как угодно близки к точке а, что может вызвать затруднения при техническом осуществлении приближения на основе данной системы функций. В таком случае всегда можно выбрать последовательность {ак}, стремящуюся к бесконечно удаленной точке, поскольку она также является точкой аналитичности интеграла Коши F(z). Не для всякой системы функций, зависящей от параметра ак, бесконечно удаленная точка будет точкой аналитичности.
Все сказанное о системе {(х - а)-1} можно применить к системе {ехр ах}, где а — комплексный параметр х е [Ь, с]. Эта система функций связана с преобразованием Лапласа, поэтому обратное преобразование может быть записано как обратное преобразование Лапласа. Но в данном случае бесконечно удаленная точка особенная и не принадлежит


Естественно возникает вопрос о нахождении коэффициентов разложения таким образом, чтобы отрезок ряда sn(x) давал как можно меньшее среднеквадратичное отклонение от f(x). Для этого разность (/ (х) - sn(x)) должна быть перпендикуляром [3] к линеалу, построенному на множестве функций ф*, где fe =1, 2.....п, другими словами, (/(х) - s„(x)) должны быть ортогональны ко всем значениям ц>к. При этом получается система линейных уравнений для нахождения коэффициентов, минимизирующих среднеквадратичное отклонение:
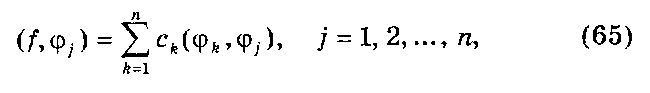
(f,g) — скалярное произведение функций f(x) и g(x).
Чтобы {ф^} были линейно независимы, достаточно взять все значения ак попарно отличными друг от друга. Система имеет единственное решение, так как ее определитель есть определитель Грама [3] и, следовательно, он больше нуля.
Докажем, что ряд, образованный с учетом полученных таким образом коэффициентов, определяет разложение f(x) в смысле L2. Ранее была доказана возможность разложения f(x) по системе {ф^}. Но по свойству перпендикуляра любая линейная комбинация из функций фА даст большее средне-
квадратичное отклонение по сравнению с проекцией функции f(x) на линеал из {фА} [3]. Следовательно, если некоторый ряд сходится к f(x), то тем более ряд с коэффициентами, определенными из условия наименьшего среднеквадратичного отклонения, будет сходиться к этой функции.
Чтобы улучшить приближение к f(x) отрезков ряда sn(x), нужно отказаться от фиксирования наперед последовательности {ак} и подбирать ее таким образом, чтобы для конечного значения п функция sn(x) давала как можно большее приближение к f{x) в смысле L2. Математически задача сводится к следующему.
Peклaмa:
