Математическое доказательство лечения неизвестных болезней неизвестными лекарствами
Решение разнообразных практических и математических задач часто обуславливает необходимость выражения различных функций тем или иным приближенным методом. В вычислительной математике разработаны методы, позволяющие осуществить требуемое приближение, например, разложения в степенные ряды, ряды Фурье по ортогональным системам функций, кусочно-линейная аппроксимация и т. д. При этом выбор вида аппроксимации определяется, в основном, из соображений математического удобства. В случае практической реализации или моделирования различных функций с помощью электротехнических устройств также используют аппроксимации в вычислительной математике.
Однако аппроксимация функций, удобная с математической точки зрения, не всегда удобна с точки зрения ее технического осуществления. Такое несоответствие возникает в первую очередь вследствие того, что вид аппроксимирующих функций, используемых в математике, существенно отличается, например, от вольт-амперных характеристик электротехнических элементов, на которых осуществляется приближение заданной функции. Поэтому возникает вопрос о возможности представления заданной функции с помощью функций, хорошо отражающих как вольтамперные характеристики реальных устройств, так и реальные функции применяемых лекарственных препаратов [2].
Рассмотрим класс функций, имеющих вид
Докажем, что линеал (совокупность всевозможных линейных комбинаций функций из множества {(х - а)"1} будет плотным в классе непрерывных функций, т. е. всегда можно подобрать такую линейную комбинацию из {(х - а)"1}, которая даст сколь угодно малое среднеквадратичное отклонение от произвольной непрерывной функции. Как известно [6], для этого необходимо и достаточно доказать, что непрерывная функция, ортогональная ко всем функциям из множества {(х - а)'1}, тождественно

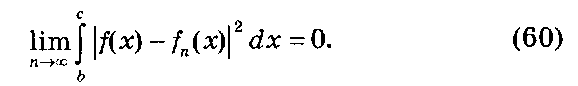
где f(x), g(x) — непрерывные функции; g(x) — комплексно-сопряженная функция g(x) [5].
Скалярное произведение дает возможность определить сходимость последовательности {fn(x)} к функции f(x) в смысле среднеквадратичного отклонения т. е. fn(x) -» f(x), если
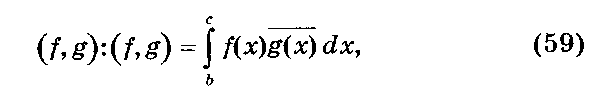
и разложения (аххп = fej)"1 на простейшие дроби описываемый класс функций сводится к классу {(х - а)"1}, где а комплексное число [3].
Покажем, что любую непрерывную функцию можно представить в виде ряда с помощью функций из множества {(*- а)'1} [4].
В пространстве функций, непрерывных на отрезке [Ь, с], введем скалярное произведение
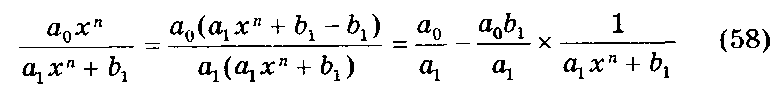
где х — аргумент, принимающий значение из отрезка [Ь, с]; а0, аг, Ъх — коэффициенты. С помощью преобразований
равна нулю, т. е. если функция-[——dx = F(z) равна
нулю при всех значениях z вне отрезка [Ь, с], когда z находится на отрезке [Ь, с], интеграл становится несобственным, то f(x) = 0. Функция F(z) является интегралом типа Коши. Выразим функцию f(x) через F(z) по формуле f(x) = F+(x) - F_(x), где х находится в интервале [Ь, с]; F+(x) и F-(x) — предельные значения F(z) как функции комплексного переменного при стремлении z к точке х соответственно сверху и снизу от отрезка [Ь, с]; F(z) — аналитическая функция вне отрезка [о, с] [5]. По условию эта функция равна нулю, если z находится вне отрезка [Ь, с]; тогда и F±(x) = 0, а следовательно, f(x) = 0.
Peклaмa:
